En los años de secundaria aprendemos las bases de las matemáticas, que son las que nos permiten encarar con garantías el aprendizaje de los conceptos y temas que vienen en bachillerato.
Son esos conceptos de base a los que debemos darle la importancia que tienen, que es mucha, desde materias como la Física, en Cinemática, Dinámica y un sinfín de temas más, como en la Química, por ejemplo en Cinética química como en las propias Matemáticas.
Vamos a centrarnos en aprender a despejar sistemas de ecuaciones de dos ecuaciones con dos incógnitas por sus tres métodos:
- Sustitución,
- Igualación
- y Reducción.
Índice del artículo
Método de sustitución
Los pasos que debemos seguir son los siguientes:
- Escogemos una de las incógnitas (la x o la y), y la despejamos, dejando la otra incógnita al otro lado de la igualdad.
- Esa incógnita despejada, la sustituimos en la otra ecuación.
- Resolvemos la ecuación que nos queda dando un valor a la incógnita que nos queda.
- Ese valor que nos ha quedado lo introducimos en el paso 1 y conseguimos el valor de la otra incógnita.
Vamos a verlo con un ejemplo

Paso 1:

Paso 2:

Paso 3:

Paso 4:

Método de igualación
Los pasos que debemos seguir son los siguientes:
- Escogemos de ambas ecuaciones la misma variable (x o y), despejamos en ambas ecuaciones la incógnita en función de la otra.
- Esas dos incógnitas despejadas, las igualamos entre sí.
- Resolvemos la ecuación resultante y damos el valor de la incógnita.
- Con ese valor lo metemos en cualquiera de las ecuaciones del paso 2, y resolvemos el valor de la otra incógnita.
Vamos a verlo con un ejemplo

Paso 1:

Paso 2:

Paso 3:

Paso 4:

Método de reducción
Los pasos que debemos seguir son los siguientes:
- Escogemos una de las incógnitas, y multiplicamos cada una de ellas por un número que me permita tener la misma incógnita de ambas ecuaciones con un coeficiente común (es decir, el mismo número multiplicando).
- Hacemos la suma o la resta correspondiente para eliminar la incógnita seleccionada (x o y).
- Resolvemos la ecuación que nos queda y damos el valor de la incógnita.
- El valor que nos ha quedado lo sustituimos en cualquiera de las ecuaciones del principio y conseguimos el valor de la otra incógnita.
Vamos a verlo con un ejemplo

Paso 1:

Paso 2:

Paso 3:

Paso 4:

En el siguiente enlace puedes ver un ejemplo de un sistema de ecuaciones resuelto por el método de reducción:
👉Consulta nuestras academias:

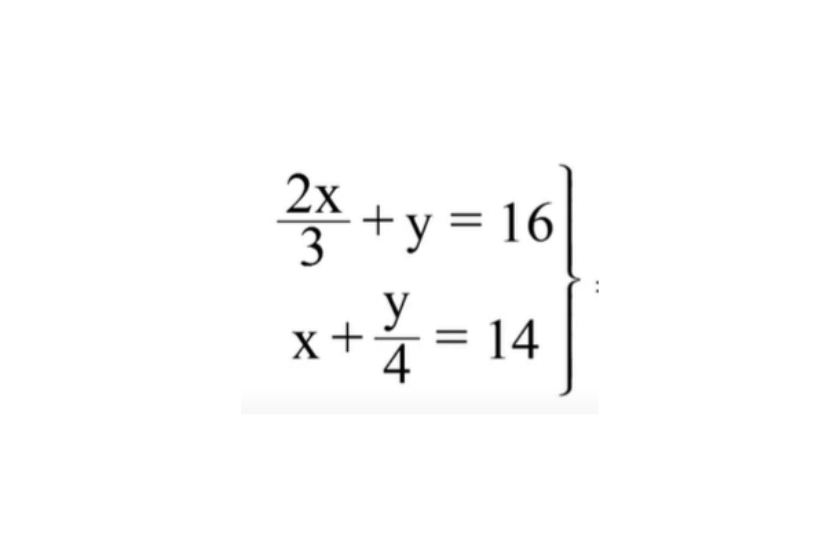


Deja una respuesta