La potenciación, o las potencias, es una operación matemática que tiene un gran impacto en la vida diaria: desde predecir modelos económicos o calcular intereses bancarios, pasando por poder calcular la propagación de una cepa de virus como sucede en la actualidad, hasta hacer simulaciones de cálculos astrofísicos, y múltiples usos más.
Índice del artículo
Definición de potencia
La potenciación es la multiplicación de un número por sí mismo repetidas veces. El número que vamos a multiplicar se llama base; la cantidad de veces que lo vamos a multiplicar lo define el número que se llama exponente.
Veamos el siguiente ejemplo:
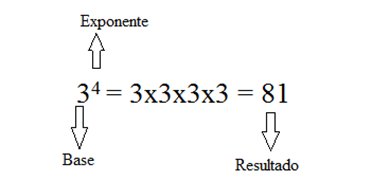
Propiedades de las potencias
Para poder operar con las potencias, lo primero e imprescindible es conocer sus propiedades. Vamos a verlas con ejemplos de cada una:
Potencia de exponente cero
a0 = 1
Cualquier número elevado a cero es igual a la unidad: 30 = 1
Potencia de exponente uno
a1 = a
Cualquier número elevado a la unidad da por resultado el mismo número: 31 = 3
👉Consulta nuestros niveles:
Producto de potencias
amxan = am+n
Los exponentes se suman mientras la base sea la misma: 24x26 = 28
(axb)m = amxbm
En una multiplicación de varias bases elevados a un mismo exponente, se eleva cada elemento de la base al exponente: (3×5)4 = 34x54
Potencia de una potencia
(am)n = amxn
Se multiplican los exponentes, por ejemplo: (32)5 = 32×5 = 310
Existen un par de casos a tener en cuenta:
- Si la base es negativa y el exponente par, el resultado es una potencia par, con base positiva: (-3)2 = 32
- Si la base es negativa y el exponente impar se deja la base con signo negativo: (-3)3 = -(3)3
División de potencias

Para dividir potencias con la misma base restamos los exponentes, por ejemplo:

Potencia de un cociente
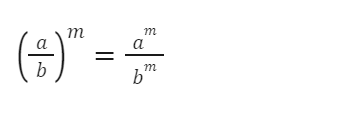
Un exponente que afecte a un paréntesis, afecta a cada término del paréntesis, ejemplo:

Potencia de exponente negativo

Un número elevado a un número negativo se puede transformar en positivo dándole la vuelta a la base:

Otro ejemplo:
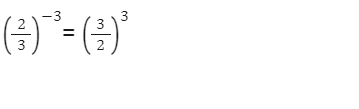
Potencia de exponente racional
Es una potencia cuyo exponente es una fracción.

Podemos convertir una raíz en una potencia, y una potencia con exponente racional en una raíz:

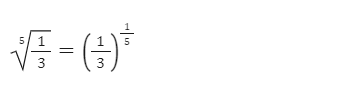
En mundoestudiante contamos con profesionales especializados en Matemáticas. Si necesitáis que os echemos una mano, reservad vuestra clase de prueba gratuita para que podamos valorar vuestra necesidades y os demos el mejor servicio. ¡Os esperamos!



Hola,
Tenéis una errata bastante importante en vuestros apuntes, ya que mezclais los conceptos de base y exponente de las potencias.
a^0 no es una potencia de base cero –> es una potencia de exponente cero
a^1 no es una potencia de base uno –> es una potencia de exponente uno
Buenos días, Penélope.
Tienes toda la razón. a^0 es una potencia de exponente cero, y a^1 una de exponente 1. Disculpa el error, lo modificamos ahora mismo.
¡Gracias!
Cómo calcular la potencia cuando el exponente=0,725
Hola Greither, cuando tenemos potencias con decimales lo primero que debemos hacer es pasar los decimales a fracción, para poder utilizar la expresión de una potencia de exponente racional.
Esperamos haberte ayudado. Un saludo.
Tienen un error en el ej de «Producto de potencias»
Puesto que «Los exponentes se suman mientras la base sea la misma:
2⁴x2⁶ = 2⁸ está mal
EL RESULTADO CORRECTO ES:
2⁴X2⁶ = 2¹⁰
Muchas gracias Santiago, pasamos a revisarlo. Un saludo.
muchisimas gracias.
gracias a esto saque un 10 en el examen y me compraron un patinete electrico .
¡Gracias a ti! Nos alegra haberte ayudado. Un saludo.
potencias jaja