¿Qué es esto de la trigonometría?

La trigonometría es una parte de las matemáticas que estudia los triángulos, especialmente los que tienen un ángulo de 90 grados, llamados rectángulos. Se estudian mediante tres ideas o magnitudes principales llamadas seno, coseno y tangente.

Pero no se trata solo de triángulos bonitos: la trigonometría es como tener superpoderes para medir cosas sin tocarla. Por ejemplo:

• ¿Quieres saber cuánto mide un árbol sin subirte?
• ¿O la distancia entre dos puntos lejanos?
• ¿O cómo se mueve un personaje en un videojuego?

¡Entonces estás usando trigonometría!

¿Qué es el seno, coseno y tangente?

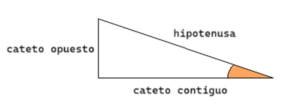
En un triángulo rectángulo, hay tres lados importantes:

• Hipotenusa: el lado más largo, el que está frente al ángulo recto.
• Cateto opuesto: el lado que está frente al ángulo que estás mirando.
• Cateto adyacente: el lado que está pegado al ángulo (junto a él).

Ahora vienen las tres palabras mágicas de la trigonometría:

Seno

Es la relación entre el cateto opuesto y la hipotenusa.

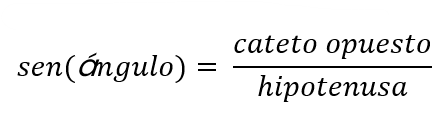
Coseno

Es la relación entre el cateto contiguo y la hipotenusa.

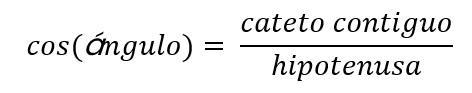
Tangente

Es la relación entre el cateto opuesto y el cateto contiguo.

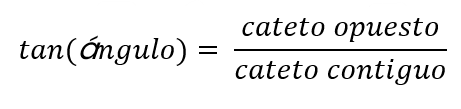
Aunque suenen raros, estos tres conceptos sirven para resolver triángulos y calcular cosas que parecen imposibles a simple vista.

Un dato curioso para entender mejor todo esto…

¿Sabías qué, aunque cambies el tamaño de un triángulo rectángulo, el seno, coseno y tangente del mismo ángulo siguen valiendo lo mismo?

Sí, suena raro, pero es lo que hace especial a la trigonometría. Si haces un triángulo con un ángulo de 30°, y luego haces otro triángulo mucho más grande, pero con el mismo ángulo de 30°, ¡las proporciones entre los lados siguen siendo las mismas!

Por eso el seno de 30° vale siempre 0,5, sin importar si tu triángulo mide 3 cm o 300 metros.

Eso significa que la trigonometría no depende del tamaño, ¡sino del ángulo!

Frase para recordar: En trigonometría, los ángulos mandan, y los triángulos siempre obedecen.

¿Y para qué sirve esto en la vida real?

Aunque suene a “palabra complicada”, la trigonometría se usa en muchos ámbitos de la vida real. No es solo para matemáticos.

Imagina que vas conduciendo por una carretera de montaña. La carretera sube formando una cuesta con un ángulo de inclinación, por ejemplo, 30° respecto al suelo plano.

Ahora imagina que esa cuesta mide 100 metros de largo (siguiendo el asfalto). La pregunta es:

¿Cuánta altura estás ganando realmente al subir la cuesta?

Aquí entra el seno:

• El seno del ángulo te dice qué proporción de la longitud de la cuesta se convierte en altura.

En este caso:

Altura = 100 · sen 30 = 50 metros

O sea, aunque recorres 100 metros por la carretera, solo subes 50 metros de altura real.

• El coseno del ángulo te diría cuánto avanzas en dirección horizontal (como si miraras la proyección de la cuesta desde arriba).

Avance horizontal = 100 · cos 30 ≈ 86,66 metros

Y te estarás preguntando, ¿y esto, para qué me sirve? Pues muy fácil; cuánto más subes, más frío hace. Y saber cuánta altura vas a ganar te puede ayudar a saber qué ropa llevar en la mochila. Porque no es lo mismo estar a 200 metros de altitud que a 1.000: ¡arriba hace más rasca!

Aquí te dejamos algunos ejemplos sencillos donde la trigonometría se vuelve super útil:

Medir cosas sin tocarlas

¿Quieres saber cuál es la altura de un edificio, una montaña o un árbol sin esfuerzo? Con trigonometría, basta con conocer el ángulo con el que estás mirando y una distancia.

Videojuegos y animaciones 3D

Los movimientos de personajes, la forma en que se ve una cámara, o cómo rebotan objetos… todo usa trigonometría por debajo.

Arquitectura e ingeniería

Diseñar puentes, rampas o escaleras, implica calcular ángulos y longitudes con trigonometría.

Física, astronomía y más ciencias

Estudiar ondas, luz, sonido, órbitas de planetas… todo eso necesita ángulos y proporciones que la trigonometría puede resolver. Yéndonos lejos, uno de los métodos para conocer distancias de planetas y estrellas es a través de dos o más telescopios situados en diferentes puntos de La Tierra. A este método se le llama triangulación.

Móviles y GPS

Funcionan con cálculos basados en ángulos y distancias.

¿Por qué aprender trigonometría?

Porque te entrena la mente para pensar con lógica, resolver problemas del mundo real y comprender el mundo de manera más profunda. Y además… ¡Es más fácil de lo que parece cuando lo ves con ejemplos!

En resumen, en mundoestudiante nos encanta enseñarte que la trigonometría no son sólo fórmulas raras, sino una herramienta genial para entender el mundo desde otro ángulo.